线性回归的两种求解方式总结
回归性能评估
均方误差

梯度下降 & 正规方程 の 均方误差
# 波士顿房价数据集
from sklearn.datasets import load_boston
# 拆分数据集
from sklearn.model_selection import train_test_split
# 标准化
from sklearn.preprocessing import StandardScaler
# 线性回归API 包含 正规方程和梯度下降
from sklearn.linear_model import LinearRegression, SGDRegressor
# 回归性能分析 (均方误差)
from sklearn.metrics import mean_squared_error
def mylinear():
"""
线性回归直接预测房子价格
:return: None
"""
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 进行标准化处理 目标值也要进行标准化处理
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# estimator预测
# 正规方程求解方式预测结果
lr = LinearRegression()
# 预估器
lr.fit(x_train, y_train)
y_lr_predict = lr.predict(x_test)
# 权重参数
print(lr.coef_)
print("正规方程测试集里面每个样本的预测价格:", std_y.inverse_transform(y_lr_predict))
print("正规方程预测的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
# 梯度下降求解方式预测结果
# 默认学习了0.01
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
y_sgd_predict = sgd.predict(x_test)
print(sgd.coef_)
print("梯度下降测试集里面每个样本的预测价格:", std_y.inverse_transform(y_sgd_predict))
print("梯度下降预测的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
return None
if __name__ == "__main__":
mylinear()
运行结果
正规方程测试集里面每个样本的预测价格: [[29.59528158]
[15.8892332 ]
[18.99740929]
[14.61008872]
[23.38270204]
[15.29248113]
[ 7.79300837]
[17.36133567]
[30.99190921]
[28.24907097]
[24.24748908]
[25.75943921]
[13.9820081 ]
[19.80078274]
[ 8.11721526]
[12.90154465]
[22.16733872]
[24.22401628]
[18.48859514]
[28.88107816]
[16.87069737]
[23.08775769]
[26.18659447]
[14.88944978]
[30.42664594]
[16.65953306]
[30.23027497]
[13.60446085]
[18.95327261]
[24.73537357]
[31.82194242]
[23.18072002]
[19.31634423]
[31.08277337]
[18.60118031]
[40.4189654 ]
[31.23171147]
[13.81568745]
[26.75510129]
[23.54932606]
[20.82637102]
[29.92258101]
[17.89884936]
[22.59411056]
[16.88970644]
[20.32039352]
[22.80539043]
[21.21869694]
[28.30762489]
[18.99391549]
[32.68201591]
[34.53044966]
[37.05822945]
[23.82503841]
[19.85776304]
[19.97788226]
[13.93488834]
[14.76014038]
[15.40201752]
[19.65444265]
[ 1.80598128]
[19.34080855]
[33.91608547]
[23.01107945]
[24.16724001]
[17.09202846]
[27.09313174]
[17.94171859]
[22.79725603]
[28.57309597]
[22.13524094]
[17.40244758]
[16.1980285 ]
[22.58083052]
[20.84107717]
[21.14477267]
[23.55265776]
[39.936372 ]
[32.09429927]
[19.69142657]
[33.75309739]
[20.83599623]
[36.44617996]
[20.47952344]
[34.90171274]
[23.5015308 ]
[12.2766674 ]
[31.13100946]
[15.77321152]
[23.0029092 ]
[27.16782406]
[22.07732113]
[20.24769687]
[28.00128307]
[14.19142358]
[23.57500996]
[19.46227382]
[35.49577061]
[17.1500728 ]
[27.57030826]
[22.01912424]
[15.93111295]
[24.2857843 ]
[15.47453586]
[19.76696051]
[ 4.12702302]
[28.06879564]
[14.74911731]
[24.99555095]
[19.20207338]
[36.83853907]
[14.37233552]
[29.76065196]
[14.91287174]
[19.41200606]
[21.07820425]
[38.90486444]
[39.10442808]
[19.80313644]
[20.40602643]
[24.55744983]
[18.08029455]
[25.06517325]
[12.79039837]
[24.85200743]
[16.29895748]
[19.99473554]]
正规方程预测的均方误差: 617.262384966235
[-0.04951063 0.06291799 -0.0425009 0.08955499 -0.08734173 0.33608833
-0.01984998 -0.21139761 0.07671246 -0.06865679 -0.1873883 0.10239201
-0.37015974]
梯度下降测试集里面每个样本的预测价格: [28.38548692 14.55454795 18.41006271 15.74078178 23.4040369 15.57854668
8.67137714 17.73301569 30.02956904 29.27338709 23.54266855 24.75302103
16.1764728 20.01910226 8.10519166 14.01279681 23.6770964 26.45061304
16.86438982 32.23686771 17.22094331 20.29967258 26.31990262 11.6108171
30.07915186 17.69413978 30.71552762 14.50241757 19.44084658 24.7652358
32.44822027 23.79208038 19.99197976 29.40686765 19.68139519 40.82953208
31.32636328 14.66863445 26.41214743 23.41647517 21.98978708 31.18421122
18.14059006 20.97997372 14.65147908 20.16414538 22.76129111 22.37091506
27.28937698 19.53393742 30.33348899 34.1711159 35.70392573 23.8143436
20.60948638 20.75920706 14.56805279 15.44977354 17.95692069 23.27529545
0.33077046 19.60773073 32.90084063 21.66470488 24.32686134 17.1905637
27.59501582 17.55911297 22.84195729 28.25059354 24.83708285 18.83851444
18.46700991 22.30646242 23.36537159 21.55669593 23.99353038 40.55485506
31.18804829 20.68783202 33.95002097 21.4608886 35.94686475 21.37460735
33.79810271 25.01058091 12.29098244 30.7545492 16.10714604 22.18214901
24.78905244 21.53431112 21.75858254 27.04666399 13.42948882 23.77622418
19.83168294 35.43803732 17.29366196 27.42613617 21.9120859 17.22861156
24.92336882 16.37287956 18.88721783 4.90444111 28.03403857 16.99450981
25.17032033 20.1064074 36.52177412 12.54585261 31.28120616 16.71943024
20.58843265 19.63703553 38.2841797 39.21331074 22.57668773 20.84362475
24.7158061 18.70070037 25.33019946 13.50257608 25.04234523 14.58382676
19.95553546]
梯度下降预测的均方误差: 616.5348148756201对比
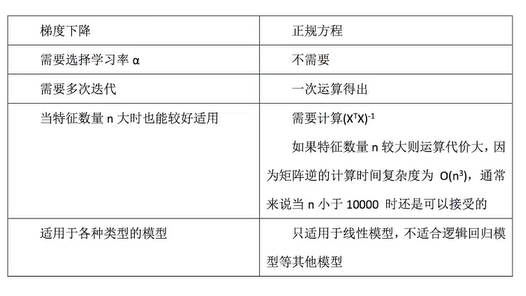
总结

用了一个多月时间 终于把黑马的 << 七天机器学习入门 >> 视频终于看完了, 视频内容有丢失, 接下来是查漏补缺.
评论已关闭
